C语言和python运行速度的比较

C语言和python运行速度的比较

今天在利用python算圆周率的过程中，发现python速度过慢，于是寻找运行速度快的语言。

发现C语言最快，据称效率是python的70倍。哪种编程语言的运行效率最高？更值得学习? - 程序员编程指南的回答 - 知乎

然后，我做了一个测试。代码思路源自 蒙特卡罗算法 - ARGO创新实验室的文章 - 知乎

首先是python的程序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import random
import math
import xlwt
import time

# def main():
t0=time.time()
print('显示程序开始的时间:',time.strftime('%Y-%m-%d %H:%M:%S',time.localtime(time.time())))
total = 0
print('Start experiment: ')
n = 0
f = xlwt.Workbook()
sheet1 = f.add_sheet('sheet1',cell_overwrite_ok=True)

for n in range(20, 10000):
    for i in range(n):
        x = random.uniform(-1,1)
        y = random.uniform(-1,1)
         
        if math.sqrt(x ** 2 + y ** 2) <= 1.0:
                        total += 1
    mypi = 4.0 * total / n
    s=abs(math.pi - mypi) / math.pi
    t1=time.time()
    sheet1.write(n,0,n)#第n+1行第1列
    sheet1.write(n,1,mypi)#第n+1行第2列
    sheet1.write(n,2,s)#第n+1行第3列
    sheet1.write(n,3,(t1-t0))#第n+1行第4列
  
    total=0



t1=time.time()
f.save('test1.xls')
print('显示程序结束的时间:',time.strftime('%Y-%m-%d %H:%M:%S',time.localtime(time.time())))
print("用时：%.6fs"%(t1-t0))

其次是C语言的程序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<stdio.h>
#include<math.h>
#include <stdlib.h>
#include <string.h>
#include<time.h>
#include <windows.h>

#define pi acos(-1)

int main(){
	LARGE_INTEGER t1, t2, tc;
    QueryPerformanceFrequency(&tc);
    QueryPerformanceCounter(&t1);
	int n, i, total;
	double x, y, mypi, s, a;
	FILE *fp = NULL ;
    fp = fopen("..\\test.xls","w") ;\\这一句我打了码
	srand((unsigned int)time(NULL));
	total = 0;
	for (n = 20;n <= 10000;n++) {
		
		for (i = 0; i < n; i++) {
			x = 2.0 * rand()  /(double)(RAND_MAX) -1 ;
			y = 2.0 * rand()  /(double)(RAND_MAX) -1 ;
			if (sqrt(x * x + y * y) <= 1.0) {
				total = total + 1;
			}
		}
		s=0;
		mypi = 4.0 * total / (n*1.0);
		s = fabs(pi - mypi) / pi;
		QueryPerformanceCounter(&t2);
		fprintf(fp,"%d\t%f\t%f\t%lf\n",n, mypi, s,(double)(t2.QuadPart-t1.QuadPart)/(double)tc.QuadPart) ;
		total=0;
		
	}
	fclose(fp);
	
    QueryPerformanceCounter(&t2);
    printf("Proceed Time: %lfs",(double)(t2.QuadPart-t1.QuadPart)/(double)tc.QuadPart);
	return 0;
}

最后发现两者差距确实大，但是在我这个环境下没有70倍这么夸张，应该只有20倍——这是检验10000个随机数后的结果，如果python要100000个excel写入程序会报错。

最后，用C成功运行了100000个随机数的情况，共计用时643.7486s。在计算到70000随机数时，粗略估计了一下计算机的处理速度，大概1s处理100个随机数；而在python那边，运行到64000随机数时，大概1s处理5个随机数。所以，总的来看，对于这个程序，很可能在极限状态下，C的效率最终为python的20倍。

最后，运用matlab分析了“随机数越大，结果越接近圆周率”这一结论——这一命题的关键预设是概率的一个命题——因为误差值普遍上比较接近，所以处理为\(e^x\)后，再进行拟合分析。

以下为matlab的代码：

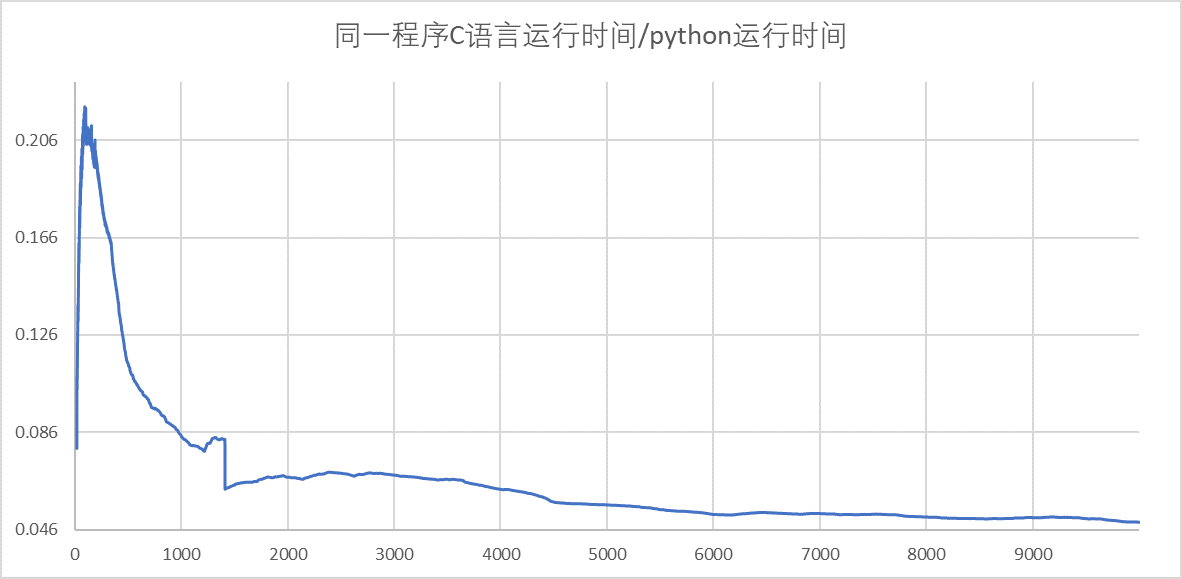
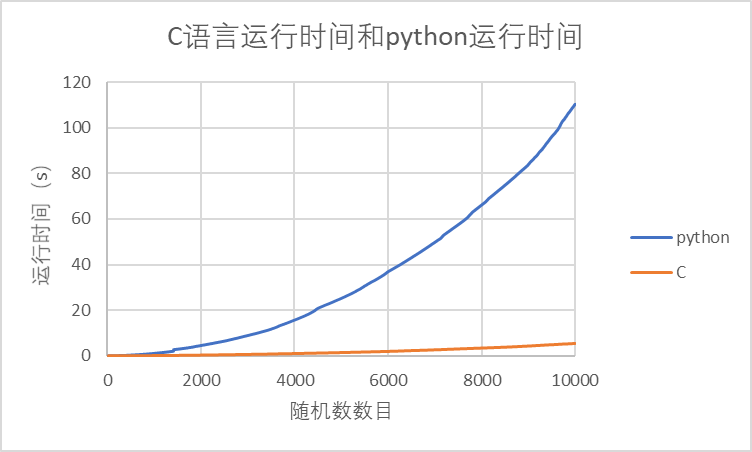
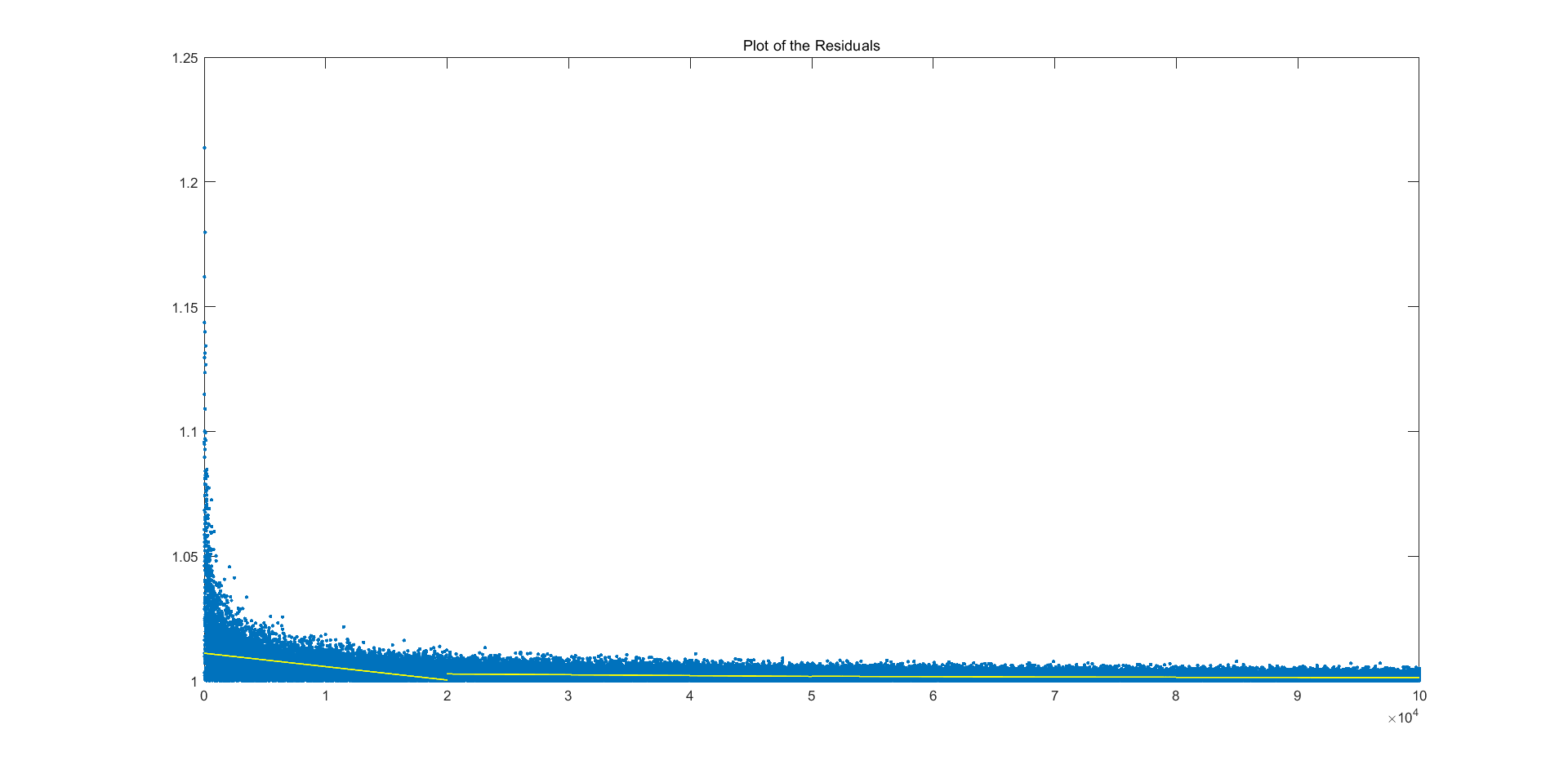
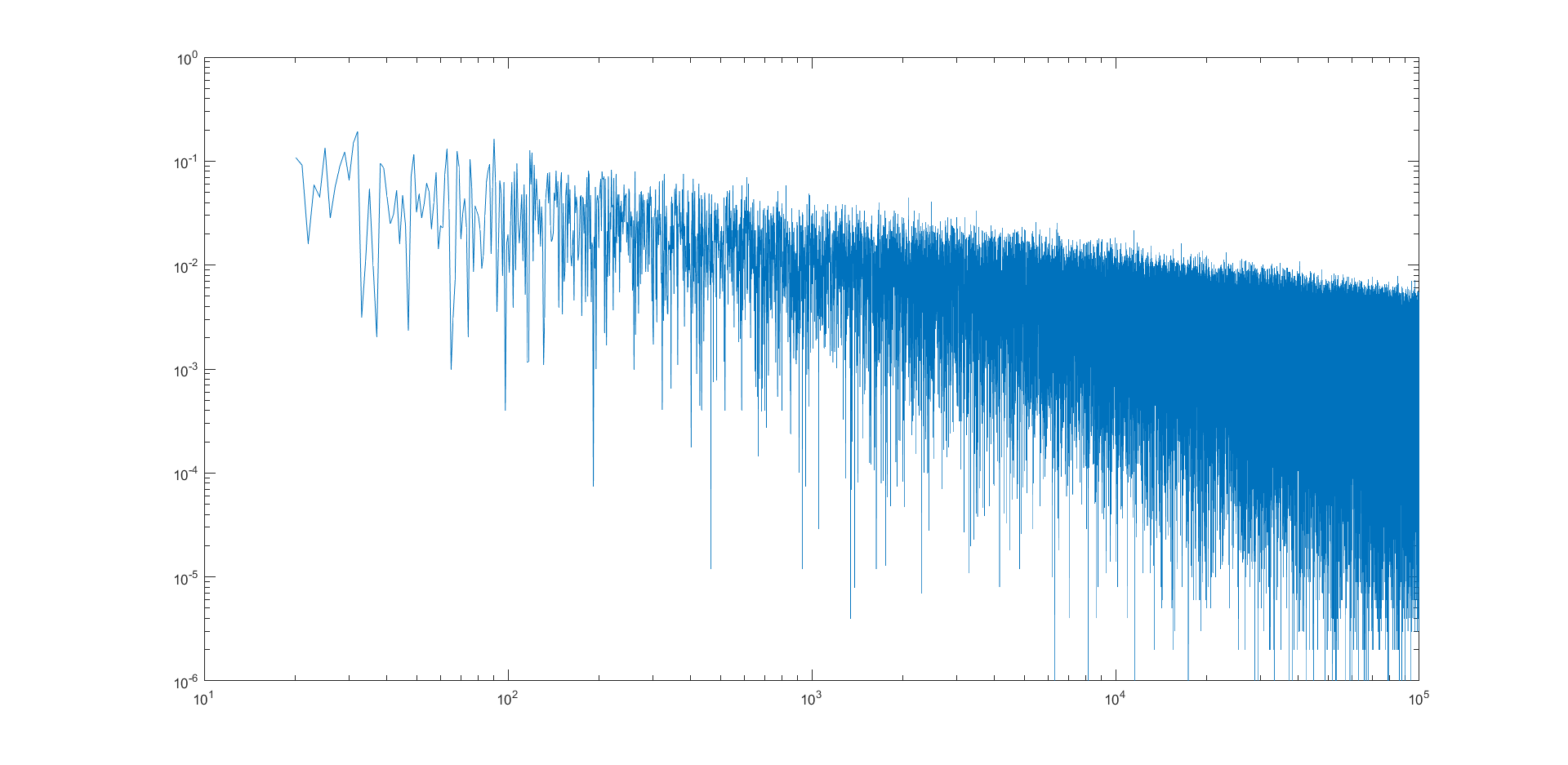
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
n=1;
p=zeros(1,n+1);
b='x^';
p = polyfit(mc.VarName1(1:20000),exp(mc.VarName2(1:20000)),n);%这一步得到拟合曲线公式，n代表n次项。t=mc.VarName1, y=mc.VarName2
t2 = 20.0:0.001:20000;%这是一种数组表示方式，0.1为步长
y2 = polyval(p,t2);%按照均匀步长得到一条拟合曲线用于绘图——由于不能直接把函数画上去
p = polyfit(mc.VarName1(20001:50000),exp(mc.VarName2(20001:50000)),n);%这一步得到拟合曲线公式，n代表n次项。t=mc.VarName1, y=mc.VarName2
t3 = 20001.0:0.001:50000;%这是一种数组表示方式，0.1为步长
y3 = polyval(p,t3);%按照均匀步长得到一条拟合曲线用于绘图——由于不能直接把函数画上去
p = polyfit(mc.VarName1(50001:60000),exp(mc.VarName2(50001:60000)),n);%这一步得到拟合曲线公式，n代表n次项。t=mc.VarName1, y=mc.VarName2
t4 = 50001.0:0.001:60000;%这是一种数组表示方式，0.1为步长
y4 = polyval(p,t4);%按照均匀步长得到一条拟合曲线用于绘图——由于不能直接把函数画上去
p = polyfit(mc.VarName1(60001:70000),exp(mc.VarName2(60001:70000)),n);%这一步得到拟合曲线公式，n代表n次项。t=mc.VarName1, y=mc.VarName2
t5 = 60001.0:0.001:70000;%这是一种数组表示方式，0.1为步长
y5 = polyval(p,t5);%按照均匀步长得到一条拟合曲线用于绘图——由于不能直接把函数画上去
p = polyfit(mc.VarName1(70001:80000),exp(mc.VarName2(70001:80000)),n);%这一步得到拟合曲线公式，n代表n次项。t=mc.VarName1, y=mc.VarName2
t6 = 70001.0:0.001:80000;%这是一种数组表示方式，0.1为步长
y6 = polyval(p,t6);%按照均匀步长得到一条拟合曲线用于绘图——由于不能直接把函数画上去
p = polyfit(mc.VarName1(80001:90000),exp(mc.VarName2(80001:90000)),n);%这一步得到拟合曲线公式，n代表n次项。t=mc.VarName1, y=mc.VarName2
t7 = 80001.0:0.001:90000;%这是一种数组表示方式，0.1为步长
y7 = polyval(p,t7);%按照均匀步长得到一条拟合曲线用于绘图——由于不能直接把函数画上去
p = polyfit(mc.VarName1(90001:99981),exp(mc.VarName2(90001:99981)),n);%这一步得到拟合曲线公式，n代表n次项。t=mc.VarName1, y=mc.VarName2
t8 = 90001.0:0.001:99981;%这是一种数组表示方式，0.1为步长
y8 = polyval(p,t8);%按照均匀步长得到一条拟合曲线用于绘图——由于不能直接把函数画上去
figure%弹出图像框
plot(mc.VarName1,exp(mc.VarName2),'.',t2,y2,'y','LineWidth',1)
hold on
plot(t3,y3,'y','LineWidth',1)
hold on
plot(t4,y4,'y','LineWidth',1)
hold on
plot(t5,y5,'y','LineWidth',1)
hold on
plot(t6,y6,'y','LineWidth',1)
hold on
plot(t7,y7,'y','LineWidth',1)
hold on
plot(t8,y8,'y','LineWidth',1)%画线
poly2sym(p);
fprintf('\nf(x)=');
txt='';
for i=1:(n+1)
    xs='';
    if p(i)>0
        fprintf('+%g*%s%d',p(i),b,n+1-i);
        xs=['+',num2str(p(i)),num2str(b),num2str(n+1-i)];
    else if p(i)<0
        fprintf('%g*%s%d',p(i),b,n+1-i);
        xs=[num2str(p(i)),num2str(b),num2str(n+1-i)];
        else if p(i)==0
                fprintf(' ');
                xs=' ';
            end
        end
    end
    txt=[txt,xs];
end
fprintf('\n');
t=text(50000,0.1,txt);

title('Plot of Data (Points) and Model (Line)')%起标题

y3 = polyval(p,mc.VarName1);%计算在每个原x时对应的拟合曲线上的值的大小
res = mc.VarName2 - y3;%计算残差

title('Plot of the Residuals')

最终的运行结果为下图

发现最后一段的线性回归线的表达式为 \[ f(x)=-1.69747\times 10^{-9}x^1+1.00152x^0 \]

我后来换了一种方法，直接直观地看最终结果，运用matlab的loglog绘图，得到如下

用semilogx更直观

Class Notes
#Computer Science
C语言和python运行速度的比较
http://avcaleb.github.io/2022/08/26/cvspython/
作者
A. V. Caleb
发布于
2022年8月26日
许可协议