海岸动力学课程笔记
By A. V. Caleb
波浪控制方程
微幅波控制方程
基本方程得出
波浪理论有如下假定:
- 流体均质、不可压缩、密度为常数
- 无粘
- 自由水面压力均匀
- 水流运动无旋
- 海底水平、不透水
- 质量力仅为重力,表面张力、科氏力不计
- 波浪为平面运动
由4可列方程 \[ \pmb{V}=\pmb{\nabla}\phi= \frac {\partial \phi}{\partial x}\pmb{i}+\frac {\partial \phi}{\partial y}\pmb{j} \] 意味着 \[ u=\frac {\partial \phi}{\partial x},\ w=\frac {\partial \phi}{\partial z}\ \ \ (1) \]
又知原先的连续性方程为 \[ \frac {\partial \rho}{\partial t}+\frac {\partial (\rho u)}{\partial x}+\frac {\partial (\rho w)}{\partial z}=0 \] 但因为1,所以转化为 \[ \frac {\partial u}{\partial x}+\frac {\partial w}{\partial z}=0\ \ \ (2) \] 将(1)代入(2)可得 \[ \frac {\partial^2 \phi}{\partial x^2}+\frac {\partial^2 \phi}{\partial z^2}=0 \Longleftrightarrow \pmb{\nabla}\phi^2=0 \] 此即为拉普拉斯方程
另可经由复杂的推导并取大气压为0得到(伯努利方程形式) \[ \frac {\partial \phi}{\partial t}+\frac {1}{2}[(\frac{\partial \phi}{\partial x})^2+(\frac{\partial \phi}{\partial z})^2]+gz+\frac{p}{\rho}=0 \] 定解条件:
- 海底表面设为固壁,因此水质点垂直速度应为0。(这个条件本质上就是牛顿内摩擦定律所要求的。)
- 在波面处,应满足动力边界条件和运动学边界条件。(动力学边界条件的意义就是水面上压力为常数。)运动学边界条件为界面上水质点运动法向速度等于界面运动法向速度,其意义为,在流体界面上,不应有穿越界面的流动,否则界面就不能存在,即流体界面具有保持性,某一时刻位于界面上的流体质点将始终位于界面上,不能有相对法向位移。
- 流场左右端面的周期性
微幅波线性化边界条件
目标——线性化自由水面边界条件以及解决不确定的边界问题,在上一部分基础上给出完整的控制方程与微幅波设定下的定解条件。
注意到自由水面边界条件非线性。且边界不确定。
把上述条件线性化,利用摄动法(也就是微幅波的本质)……因为过于复杂,就不展示了(具体过程的图放在附录里)……
可以得到最后的结果
控制方程及其定解条件(微幅波设定下)
$$ ^2 。意义:该运动为无旋,液体不可压缩\
=0, z=-h。意义:海底表面设为固壁,因此水质点垂直速度应为0。\
+g=0, z=0。意义:自由水面运动边界条件。利用摄动法,只考虑一阶近似解。 \上一个式子本质上由-=0,z=0与下面一个式子联立而得\
=-, z=0。意义:动力边界条件,由摄动法求出,引入了微幅波。\
(x,z,t)=(x+L,z,t)=(x,z,t+T)。意义:流场左右两端面的边界条件。\ $$
微幅波理论解
假设速度势函数 \(\phi (x,z,t)=X(x)Z(z)T(t)\)——需要知道这只是一种近似的处理——然后通过解偏微分方程再联立边界条件,最后得到色散方程 \[ \sigma^2=gktanhkh \] 其中 \[ \sigma=\frac{2 \pi}{T},\ k=\frac{2\pi}{L} \] 代入可得 \[ \begin{array}{cc} L=\frac{gT^2}{2\pi}tanhkh \\ c=\frac{gT}{2\pi}tanhkh \end{array} \] 如此,从色散方程的本质可以看出,当水深给定时,波的周期越长,波长越长,波速也越大,这样就使不同波长的波在传播过程中逐渐分离开来。这种现象也就使波的色散现象。同时其还表明,波浪的传播与水深也有关。
深水波
\(h>L/2\)时,可以认为处于深水情况。
这时,色散方程转化为 \[ \sigma^2=gk \] 等价式为 \[ \begin{array}{cc} L_0=\frac{gT^2}{2\pi} \\ c_0=\frac{gT}{2\pi} \end{array} \] 从而深水情况下,波速与波长只与周期有关,与水深无关。
浅水波
\[ \begin{array}{cc} \sigma^2=gk^2h \\ L_s=T\sqrt{gh},\ c_s=\sqrt{gh} \end{array} \]
从而,浅水波的波速只与水深有关。
水质点运动轨迹
水质点运动轨迹为一个椭圆,在深水情况下为一个圆。
在水面处轨迹半径为波浪振幅,随着距水面深度增大,轨迹圆的半径以指数形式迅速减小。
波浪压力由静水压力和动水压力两部分组成,压力响应系数随着质点位置深度增大而迅速减小。
微幅波单宽波峰线长度一个波长范围内平均的波浪动能和势能相当。
立波的势能及动能都为行进波的两倍。
能量的转化是周期性地由动能转化为势能,或由势能转化为动能。
斯托克斯波理论
波峰变得尖陡,波谷变得平坦。波峰波谷不再对称于静水面。
斯托克斯波不适用于浅水。
水质点运动轨迹不封闭
浅水非线性理论
是一种主要的浅水非线性波理论。这一理论中波浪的各特性均可以用雅可比椭圆函数形式给出,因此命名为椭圆余弦波理论。
当波长无穷大时,椭圆余弦波趋近于孤立波。孤立波是一种推移波,水质点只朝波浪传播方向运动而不向后运动。随着波峰到来,水质点作向上和向前运动,在波峰通过时刻,水平质点速度达到最大值,垂直速度为0,质点向上位移达到最大。在波峰通过以后,水质点开始下降,水平质点速度逐渐慢下来,最后回复到原水质点深度位置上,但在水平方向上水质点有一个水体净向前位移。
实际上几乎绝大部分能量都集中在波峰附近。
当振幅很小或相对水深\(h/H\)很大时,为浅水正弦波。
随机波浪理论
通常用上跨(或下跨)零点法定义波高、周期。
运用统计方法分析、运用海浪谱理论分析。以不同频率的波的能量构成一个函数,即为波频谱。由于它反映波能密度分布,所以又称能谱。
波频谱的形状与波浪的生成机理有关,主要取决于风速、风距和风时三个要素
波浪传播和破碎
浅水区波浪能量损失的形式有三种:
- 摩阻损失
- 渗透损失
- 泥面波阻力损失
后两种损失一般不计,底摩阻损失在浅水区较为显著。
波浪进入浅水区后,波高会产生变化,这种变化称为浅水变形。
规则波在变水深中传播,波速、波长、波高和波向都将发生变化,但波周期不变。
波数向量随时间变率必然为角频率的局部变化所平衡
对于稳定波浪场,波周期为常量,不随空间变化。即使水深有缓慢变化时,波周期也始终保持恒量。
波浪在浅水中传播时其波速变化只与水深有关,且与水深的平方根成正比,而与波周期或波长大小无关!
浅水变形
波浪进入浅水区后,波高会发生变化。
波高在有限水深范围内减小的原因与波能传递率有关。
波浪折射
波峰线和波向线(波数矢量相连而成的表达波浪传播方向的曲线)随水深变化而变化的现象称为波浪折射。
在海岬岬角处,波向线将集中,这称为辐聚;在海湾里,波向线将分散,称为辐散。
波浪绕射
波浪在传播中遇到障碍物如防波堤等,除可能在障碍物前产生波浪反射外,还将绕过障碍物继续传播,并在掩蔽区发生波浪扩散,这是由于掩蔽区内波能横向传播所造成,这种现象称为波浪绕射。
绕射区内的波浪称为散射波。
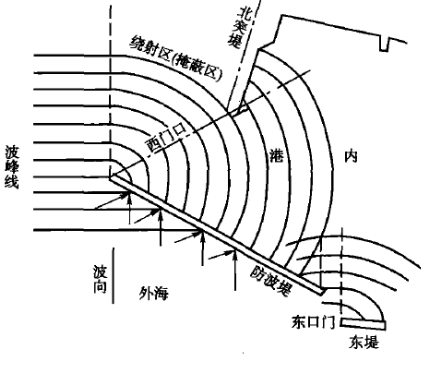
绕射区内的散射波的同一波峰线上的波高是不同的,愈深入掩蔽区内波高愈小,但其波周期则保持不变。
潮波
\[ continuity\quad equitation: \frac {\partial \eta}{\partial t}+\frac {\partial u(h+\eta)}{\partial x}+\frac {\partial v(h+\eta)}{\partial y}=0 \]
\[ Momentum\quad equitation: \begin{cases} \frac {\partial u}{\partial t}+u\frac {\partial u}{\partial x}+v\frac {\partial u}{\partial y}+g\frac {\partial \eta}{\partial x}=fv +v (\frac {\partial^2 u}{\partial x^2}\frac {\partial^2 u}{\partial y^2})-\frac {gu\sqrt{u^2+v^2}}{c^2(h+\eta)} \\\\ \frac {\partial v}{\partial t}+u\frac {\partial v}{\partial x}+v\frac {\partial v}{\partial y}+g\frac {\partial \eta}{\partial y}=-fu +v (\frac {\partial^2 v}{\partial x^2}\frac {\partial^2 v}{\partial y^2})-\frac {gv\sqrt{u^2+v^2}}{c^2(h+\eta)} \end{cases} \]
海峡之中
1.前进潮波(对上式简化的结果)
\[ \begin{cases} \frac {\partial \eta}{\partial t}+h\frac {\partial u}{\partial x}=0\\\\ \frac {\partial u}{\partial t}+g\frac {\partial \eta}{\partial x}=0 \end{cases} \Rightarrow \frac {\partial^2 \eta}{\partial t^2}+gh\frac {\partial^2 \eta}{\partial x^2}=0 \] 解方程可得: \[ \begin{cases} \eta =\frac{H}{2}Hcos(kx-wt)\\\\ U =\frac{H}{2c}Hcos(kx-wt) \end{cases} \]
2.驻波
这里假设有两列波 \[ \begin{cases} \eta_1 =\frac{H}{2}Hcos(kx-wt)\\\\ \eta_2 =\frac{H}{2}Hcos(kx-wt) \end{cases} \Rightarrow \eta=\eta_1+\eta_2=Hcos(kx)cos(wt) \] 代入 \[ \frac {\partial u}{\partial t}+g\frac {\partial \eta}{\partial x}=0 \Rightarrow u=\frac{H}{c}sin(kx)sin(wt) \]
3.变形
波能流 \[ P=ECn=\frac{1}{8} \rho gH^2 c*\frac{1}{2}(1+\frac{2kh}{sh2kh}) \]
浅水波 \[ C=\sqrt{gh}\quad n=1 \]
\[ \begin{cases} P_1=E_1\sqrt(gh_1)B_1\\\\ P_2=E_2\sqrt(gh_2)B_2 \end{cases} \quad\stackrel{P_1=P_2}\Rightarrow\quad\frac{H_2}{H_1}=(\frac{n_1}{n_2})^{\frac{1}{4}} \]
海岸波生流
海岸环流体系
- 当波浪从外海传播过来,波高有大有小,有一个向岸边的质量输移流,且流速与波高成正比,因而波高大的地方过来的水多,从而不同波高点会产生沿岸流。同时会有时不时的裂流,从流速大的点背向海岸流去。
- 然而,上述对海岸波生流的解释还非最为根本的。后来,此现象通过概念"辐射应力"得到解决。
辐射应力
在x与y轴上各有两个方向(平行某轴、垂直某轴)互相垂直的辐射应力。 \[ S= \left( \begin{array}{cc} S_{xx} & S_{xy}\\ S_{yx} & S_{yy} \end{array} \right) \]
其中 \[ S_{xx}=\frac{\iint \rho uudzdt}{T}+\frac{\iint Pdzdt}{T} \] \[ S_{yx}=\frac{\iint \rho vudzdt}{T} \] 又记得微幅波中 \[ u=u_0cos\alpha \quad v=u_0sin\alpha \] \[ P=P_0+\rho gz+\rho g k \eta \] 最后,是水体各个相对面的应力梯度推动了水体的运动。 \[ S= \left( \begin{array}{cc} ncos^2\alpha+\frac{1}{2}(2n-1) & \frac{H}{2}sin2\alpha \\ \frac{n}{2}sin2\alpha & nsin^2\alpha+\frac{1}{2}(2n-1) \end{array} \right) \]
控制方程
首先回顾方程 \[ \frac {\partial u}{\partial t}+u\frac {\partial u}{\partial x}+v\frac {\partial u}{\partial y}+g\frac {\partial \eta}{\partial x}=fv +v (\frac {\partial^2 u}{\partial x^2}\frac {\partial^2 u}{\partial y^2})-\frac {gu\sqrt{u^2+v^2}}{c^2(h+\eta)} \] 在波生流中,要加上辐射应力,因而变为 \[ \frac {\partial u}{\partial t}+u\frac {\partial u}{\partial x}+v\frac {\partial u}{\partial y}+g\frac {\partial \eta}{\partial x}=fv +v (\frac {\partial^2 u}{\partial x^2}\frac {\partial^2 u}{\partial y^2})-\frac {gu\sqrt{u^2+v^2}}{c^2(h+\eta)}+(\frac{\partial S{xx}}{\partial x}+\frac{\partial S{yx}}{\partial y}) \] 此时若对上式两边进行平均,把非线性、地转、粘性、底摩阻都忽略掉,又因为正向与x轴没有夹角,从而得到: \[ -\rho gd\frac{\partial \bar{\eta}}{x}+\frac{\partial S{xx}}{\partial x}=0 \] 其中,前者为压力,后者为辐射应力的梯度。这个方程为平衡状态。
波高越大、辐射应力越大。平均海平面指向外海。
波浪的增水和减水
对于减水,有 \[ \bar{\eta_b}\approx-\frac{H_b}{20} \]
波浪的增水——平均海平面比没有波浪的时候要高。
波浪增水的公式: \[ \bar{\eta}= \begin{cases} \bar{\eta_b}+K(h_b+xtan\beta), & x\geq x_b\\\\ -\frac{kA^2}{2sinh2kh}, & x<x_b \end{cases} \]
沿岸流
当波浪与岸的法线有夹角,
因为实际上,波浪的波高有变化,所以Y方向上的辐射应力不等于0。
本质上为由于x方向上有一个辐射应力梯度,所以推动了y方向上的流的不断的流动。
所有沿岸流都与底摩阻有关系。
考试内容
波浪控制方程、潮流控制方程、海岸波生流控制方程
附录
伯努利方程导出

