土力学细节复习札记
土力学复习札记
By A. V. Caleb
这个札记主要为了土力学中一些零零碎碎的性质。因为前几天,我已经把土力学基本的概念框架做好了。
第二章、土的物理性质与工程分类
土的三相组成
固体
一定范围粒径的土粒称为粒组。
0.005~0.075mm为粉粒
土的颗粒级配是由土的颗粒大小分析实验测定的,若小于0.075mm则一般用土粒在水中匀速下沉测得。
土粒级配曲线为粒径累积频率曲线,横坐标为对数,因为粒径相差巨大。若曲线较陡,则级配不好,因为土粒均匀。若曲线平缓,则反之。见下图
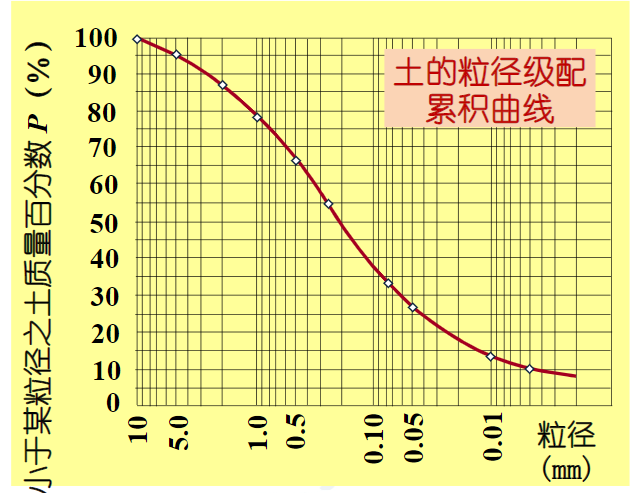
重点!小于某粒径的土粒质量累计百分数为10%时,则相应的粒径称为有效粒径\(d_{10}\)。此外,\(d_{30}、\ d_{60}、\ d_{50}\)同理。\(d_{60}\)称为限定粒径,\(d_{50}\)为平均粒径。这四个为特征粒径。
不均匀系数 \[ C_u=\frac{d_{60}}{d_{10}} \] 显然,容易推得,\(C_u\)越大,则曲线越平缓,粒径分布越均匀,级配越好。
曲率系数 \[ C_c=\frac{d_{30}^2}{d_{10}\cdot d_{60}} \] \(C_c\)则表现累计曲线的分布范围,反映曲线的整体形状。
级配良好:
- 一般情况下,将\(C_u>10\)的土视为级配良好的土。
- 一般认为,对于砾类土或砂类土同时满足\(C_u\geq 5和C_c=1\sim 3\)两个条件时,则定名为良好级配砾或良好级配砂。
关于矿物,参考下面这张图
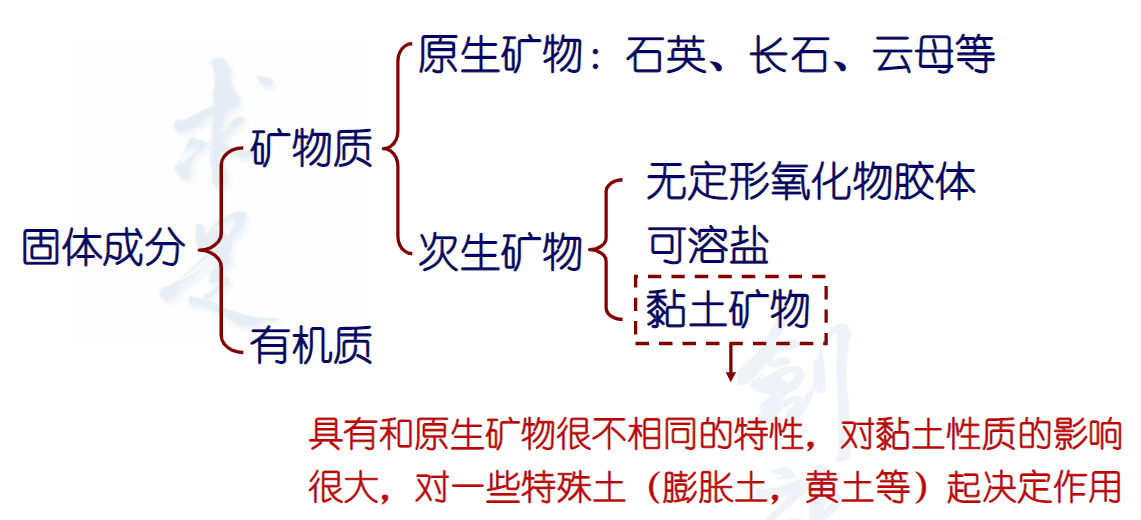
黏土矿物可分为高岭石、伊利石、蒙脱石三类。三者亲水能力依次增强,比表面积也依次增大。下面为三者颗粒形状
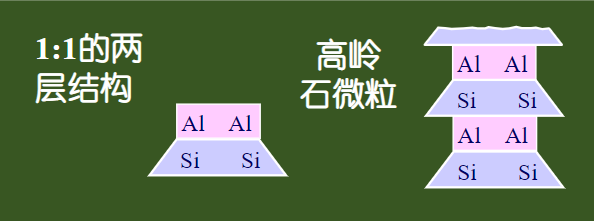
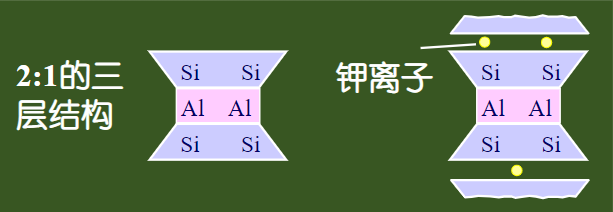
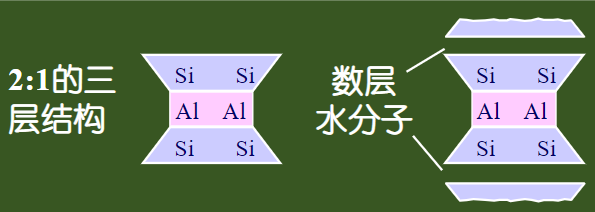
土中水
强结合水——接近固体
弱结合水——水膜,土中有较多弱结合水,则具有一定的可塑性
另外,自由水分为毛细水和重力水,重力水自由流动,毛细水承受表面张力和重力作用。
三个指数
密实度 \[ D_r=\frac{e_{max}-e}{e_{max}-e_{min}} \] 砂土可根据锤击数划分密实度,粗粒土可根基相对密度。
塑性指数(注意省去%) \[ I_p=w_l-w_p \] 塑性指数乃综合性指标,本质上为土体结合水的可能含量,与土颗粒、矿物成分、土中水的离子成分、浓度有关。
液性指数 \[ I_l=\frac{w-w_p}{w_l-w_p} \] 本质上为非常巧妙的设计:小于0时,则为半固体(坚硬状态);在0到1之间时,为可塑状态;大于1,则为流动状态。因此乃为判断稠度。
两个结构
粗粒土:单粒结构
细粒土
分散结构:分散结构的颗粒一般平行排列
絮凝结构:土的结构是面-边接触
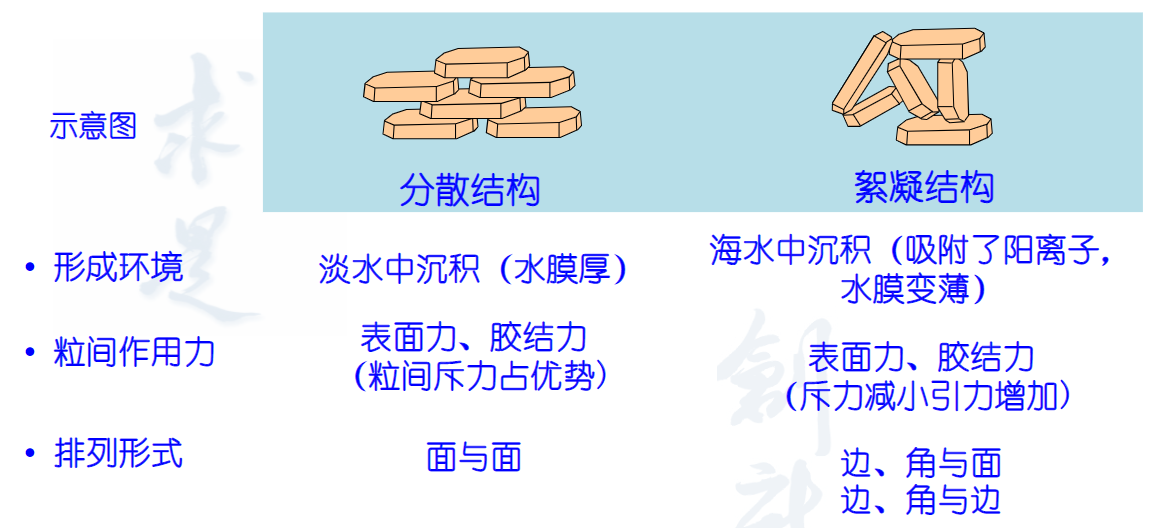
土的压实性
细粒土压实标准:压实度 \[ D_c=\frac{\rho_d}{\rho_{dmax}} \] 细粒土之所以有最优含水量是两方面:水的润滑作用、水中的空气能否排出。
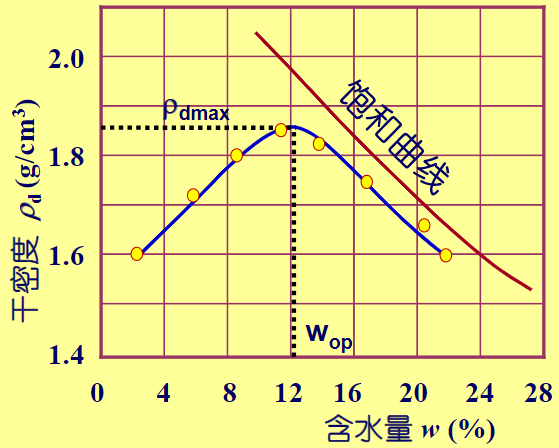
可知,最优含水量大概12%。
对于粗粒土,压实标准用相对密度\(D_r\)。一般\(D_r\)要0.7以上。
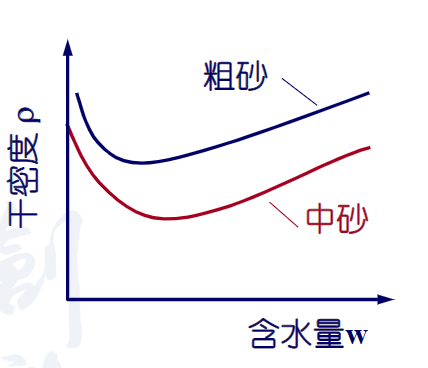
注意完全风干或饱和状态下容易击实。
土的工程分类
粗粒土:级配组成
细粒土:矿物成分、亲水性(\(I_p\))
规范中分为碎石土、砂土、粉土、黏性土
第三章、土的渗透性
渗透力:孔隙水对土骨架的拖曳和推动力、方向与水力坡降一致
土体受力分析:土骨架、土水整体为隔离体
渗透系数
温度越高,水粘滞性越低,渗透性越大
渗透系数分界值(cm/s) \[ 黏土 10^{-6}\quad 粉土10^{-4}\quad 10^{-3}\quad 砂土10^{-1} \]
流土与管涌的区别
流土是即刻因为巨力而顷刻发生的,管涌是长期掏蚀而成的。
防治措施
流土: 1. 延长上游渗径,减小下游水压 2. 下游增加透水盖重
管涌: 1. 设反滤层 2. 减小渗透坡降
有效应力原理
考试时回答方式: 1. 饱和土体任一平面的总应力都可分为有效应力和孔隙水压力(要有推导过程) \[ \sigma=\sigma'+u \] 2. 土的变形与强度都只取决于有效应力 1. 有效应力:是土体变形的原因、是土体强度的成因 2. 孔隙水压力:各个方向受力、不能承受剪力
第四章、地基土的应力计算
总应力=自重应力+附加应力
自重应力(有效应力)计算
需要注意的是,计算有效应力时,如果存在渗流情况,应当为土的自重+渗流压力。
渗透应力(注意与自重应力的方向,这里假定为相反)的求法: \[ \sigma_{jz}'=-\frac{J}{A}=-\frac{jV}{A}=-jH=-i\gamma_w H=-\gamma_w \Delta h \]
注意:考试的时候需要画不同土层的分割线以及水位线
基底压力分布
分布情况十分复杂,分为:柔性基础(不传递剪应力,应力分布与断面形状相同)、刚性基础(随荷载增大,应力分布不同)、弹性基础(处于上两者之间)
根据圣维南原理,简化可得基地平均压力 \[ P=\frac{F+G}{A} \] F为作用在基础上的竖向荷载,G为基础及回填土总重度 \[ G=\gamma_d Ad \] 一般,这里的\(\gamma_d\)取\(20KN/m^2\),在地下水位时应扣去浮力。需要注意的是,d要从设计地面算起。
又需要注意的是,计算基地平均附加压力\(p_0\)时,减去的土体原有自重应力是从天然地面算起。 \[ p_0=p-\sigma_{cd}=p-\gamma_0 d \] 在遇到天然土层有多层土时需要注意 \[ \gamma_0=\frac{\sum \gamma_i h_i }{\sum h_i} \] 由布辛涅斯科解 \[ \sigma_z=\alpha \frac{P}{Z^2} \] 则可知其应力分布情况
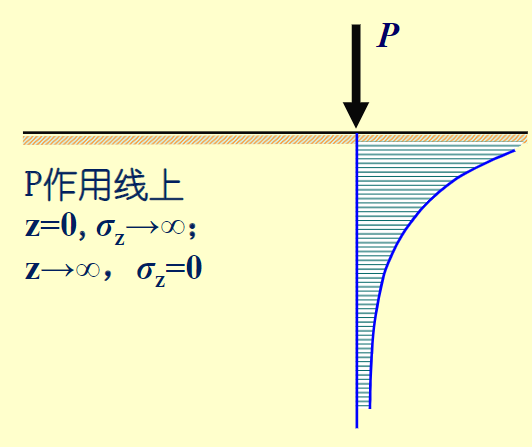
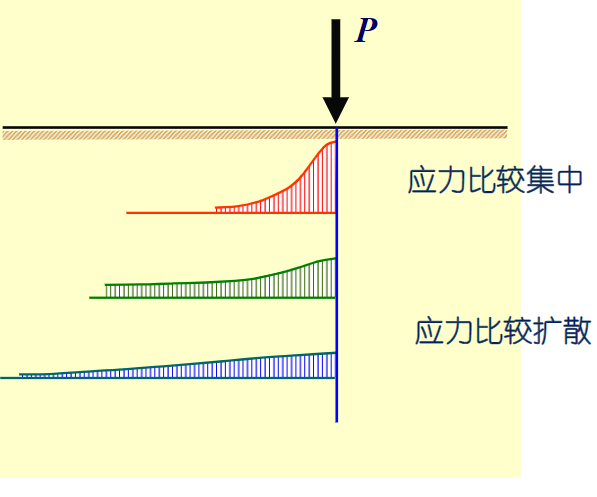
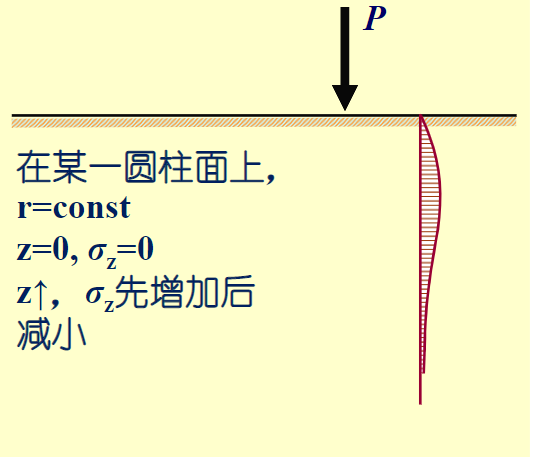
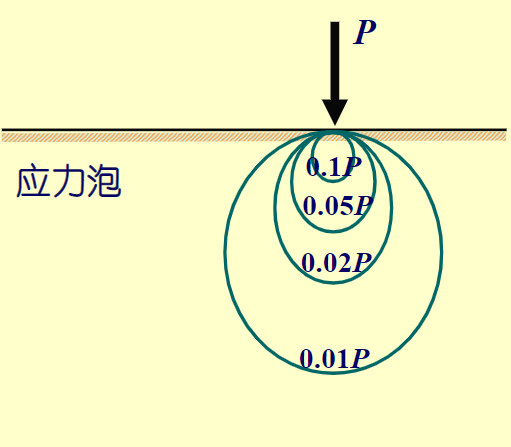
多层土的情况
如果上层土软,则其高度换算就小,就会应力集中;从而上层土硬,就会应力扩散。
均质土的情况
一般下层土会随着自重应力增加而固结,从而下层土偏硬。因而出现应力集中现象。
天然的土竖向的模量一般大于横向的模量,从而因为横向应力扩散不出去,产生应力集中。
至于非线性和弹塑性情况,因为在推到布辛涅斯克解时,与材料的弹塑性等关系不大,所以竖向应力不怎么受弹塑性影响。而因为横向压力需要乘一个侧压力系数,这个侧压力系数,侧压力系数与模量、泊松比等是有关系的,因而对水平应力有显著影响
第五章、土的压缩性和固结理论
压缩模量等都需要记忆。
\(a_{1-2}\)即应力范围为100-200kPa的a。通常也用这个a对不同土的压缩性进行比较。
需要记得的图是
e-lgp曲线主要用来研究应力历史。
土的变形模量(无侧限时测得)\(E_0\)也是需要记忆的。 \[ E_0=\frac{\Delta\sigma_z}{\Delta\epsilon_z} \] 实际上,除了变形模量\(E_0\),其它都是土的侧限压缩的指标。
常规三轴是可以被压坏的,因为旁边的压力(水压)是固定的,而不会无限支撑;而侧限压缩实验因为旁边有刚体的支护,所以不会被压坏,而存在体积压缩极限。
土的变形模量\(E_0<\)侧限压缩模量\(E_s\)
先期固结压力:土在历史上经受过的最大竖向有效应力称为先期固结压力。
超固结比 \[ OCR=\frac{p_c}{p_0} \] \(p_c\)为先期固结压力,\(p_0\)为土现在所受的竖向压力。
若\(OCR>1\),则该土为超固结土。
数学模型
连续性条件:土体的体积变化=孔隙体积变化=流入流出水量差,从而联系起土的压缩特性、有效应力原理、达西定律。从而得到渗流固结方程。
固结系数需要记 \[ C_v=\frac{k_v(1+e_l)}{a\gamma_w}=\frac{k_vE_s}{\gamma_w} \] 其中,\(k_v\)为土层竖向渗透系数。a为压缩系数。\(e_1\)相应于\(p_1\)作用下压缩稳定后的孔隙比。
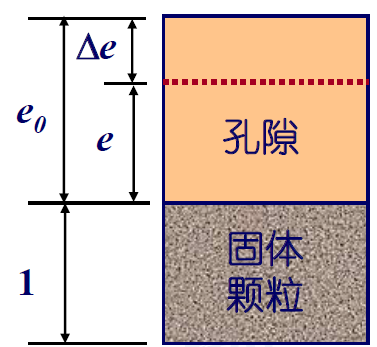
时间因子的公式自然也需要记忆 \[ T_v=\frac{C_v}{H^2}t \] 其中,\(H\)为地基土层最大竖向排水距离,又记图层厚度为\(H_s\),则对于单面排水情况,\(H=H_s\);对于双面排水情况,\(H=H_s/2\)。
此外,需要记忆固结度的概念 \[ 一点的固结度U_{z,t}=\frac{\sigma_{z,t}'}{\sigma_z}=1-\frac{u_{z,t}}{\sigma_z} \] 一般常考的是土的平均固结度 \[ 土的平均固结度=\frac{有效应力分布面积}{总应力分布面积} \] 不过,考的时候不会让算弧线面积,而是算折线包围的应力面积。
另外,重点的需要记住的是 \[ S_t=S_{\infty}\cdot U_t \] 此外,沉降量等于排出水的量,因为 \[ S_{t}=\int \epsilon_zdz \]
另有一个或许比较重要,就是下面这张图
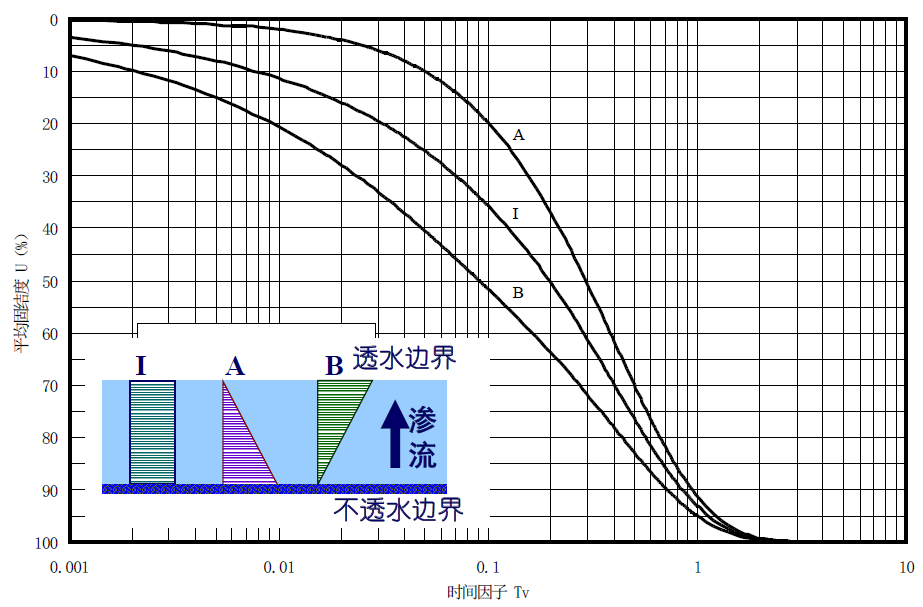
注意,当双面排水时,无论应力分布如何,都可以通过割补而成为矩形的应力分布。
同样需要注意,在一维固结理论中,初始的超静孔压也就是总应力。
最好参考一下下面这张图:
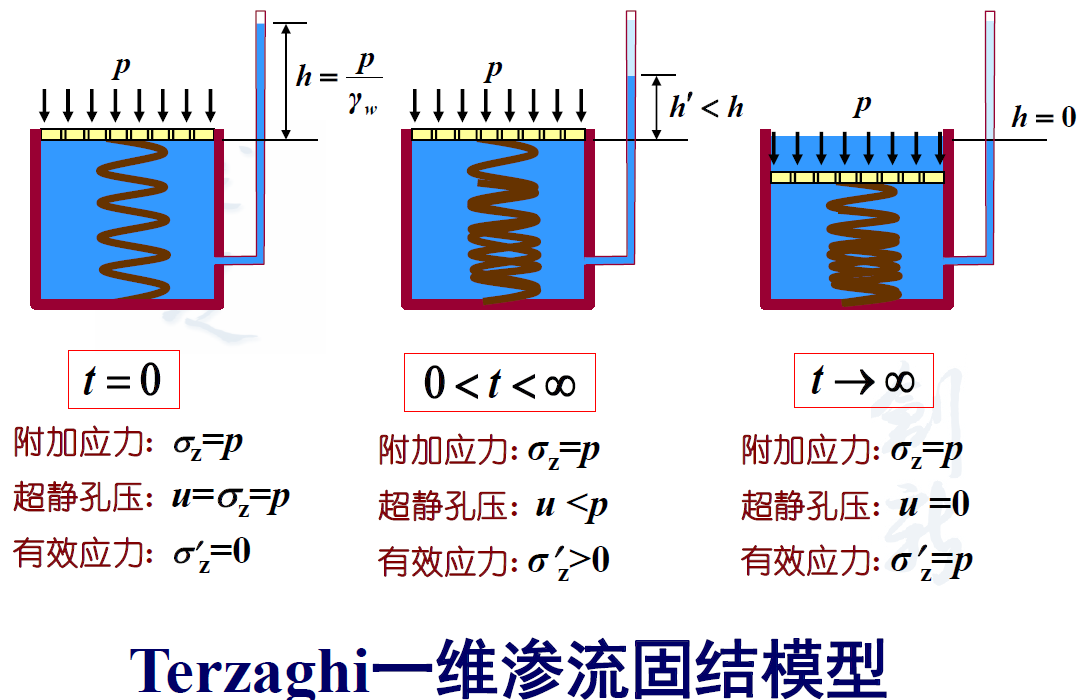
第六章、地基沉降与计算
地基沉降的基本理念借鉴于压缩试验,其假定土层压缩时不发生侧向变形
对于规范法,任意深度z范围内的压缩量为 \[ s'=\frac{p_0z\bar{\alpha}}{E_s} \] 其中,\(\bar{\alpha}\)是附加应力系数。毕竟整个公式是基于附加应力得到的,原型为\(s'=\frac{A}{E_s}\)。本质上也是分层总和法,所以结果会比较符合基础中心点下的土体状况。
则第i层土的土体压缩量为: \[ \Delta s'_i=\frac{p_0}{E_{si}}(z_i\bar{\alpha_i}-z_{i-1}\bar{\alpha}_{i-1}) \] 其中,\(E_{si}\)是第i层土的压缩量。
为提高精度,最后需要乘上修正系数。 \[ s=\psi_ss' \]
第七章、土的抗剪强度
土的抗剪强度有两个公式 \[ \begin{cases} \tau_f=c'+\sigma'tg\varphi'\\\\ \tau_f=c+\sigma tg\varphi \end{cases} \] 其中 \[ \begin{array}{cccc} c',\ \varphi'——土的抗剪强度有效应力指标\\ \sigma,\ \sigma'——作用在剪切面上的总应力和有效应力值\\ u——破坏时土体中的孔隙水压力\\ c,\ \varphi——土体抗剪强度总应力指标 \end{array} \] 同时需要注意
\[ c——土的黏聚力 \]
\[ \varphi——土的内摩擦角 \]
土的抗剪强度的测定
不固结、不排水实验的莫尔圆的规律很奇特,根本上是因为其不固结。正是因为不固结,所以总应力里包含的成分只有超孔压,而水的抗剪强度不会因为水压的增大而增大。所以导致最后的摩尔包线是水平的。如下图。
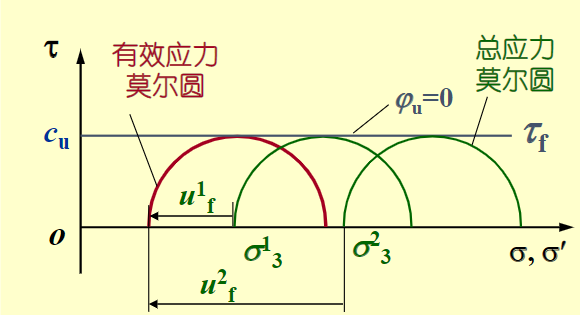
从而UU实验只用于测定饱和黏土不排水抗剪强度\(C_u\),应用于总应力等于0的情况。
不过,此处的不固结不是指土样从未固结过,而是在三轴仪中在所加压力下土体未发生排水固结。
无侧限抗压强度实验可以用来测定土的不排水抗剪强度\(C_u\)和饱和黏土的灵敏度。
十字板剪切实验比较能反映土的原位强度,一般也用于测定土的不排水抗剪强度\(C_u\)。
课程重点
固结公式——推导要记
弱结合水——决定可塑性
最有含水率——原理、机理(水膜,缩限-塑限)
固结的公式不用记
地基沉降不考计算
摩尔库伦公式要记
有可能整体圆弧法
考主动土压力